Difference between revisions of "Quantum Monte Carlo for Chemistry @ Toulouse"
(→News) |
|||
| (104 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | This website is devoted to | + | [[File:peptide_cu.png|350px|right]] |
| − | activities of the quantum Monte Carlo group of Toulouse, France. | + | This website is devoted to the scientific and software |
| − | + | activities of the quantum Monte Carlo (QMC) group of Toulouse, France. | |
| + | The grand objective of our project is to make of QMC an alternative and efficient tool for electronic structure in chemistry. Our group -- headed by Michel Caffarel -- is located at the | ||
[http://www.lcpq.ups-tlse.fr Laboratoire de Chimie et Physique Quantiques], [http://www.cnrs.fr CNRS] and [http://www.ups-tlse.fr/ Université Paul Sabatier]. | [http://www.lcpq.ups-tlse.fr Laboratoire de Chimie et Physique Quantiques], [http://www.cnrs.fr CNRS] and [http://www.ups-tlse.fr/ Université Paul Sabatier]. | ||
| + | [[File:Anr.gif|100px|center]] | ||
| − | == QMC | + | <B>The QMC=Chem project is supported by the french Agence Nationale de la Recherche Scientifique (ANR) under Grant No. ANR2011 BS08 004 01 |
| − | + | </B> | |
| + | |||
| + | == News == | ||
| + | |||
| + | * June 2015: [http://www8.hp.com/h20195/v2/GetPDF.aspx/4AA5-9253ENW.pdf Université Paul Sabatier saves space and energy with HP Moonshot] | ||
| + | |||
| + | * December 2014: QMC=Chem was selected for the France-Grilles Cloud Challenge. [https://webcast.in2p3.fr/videos-retour_dexperience_sur_lutilisation_de_services_francegrilles_projet_challenge_fg Video] | ||
| + | |||
| + | * June 2014: QMC=Chem was selected for a meso-challenge on the new CALMIP system [http://www.calmip.univ-toulouse.fr/spip/spip.php?article388 EOS]. 12000 cores ran for 48 hours. | ||
| + | |||
| + | * July 2013: QMC=Chem tutorial, Cecam workshop [http://www.cecam.org/workshop-942.html Atomistic and molecular simulations on massively parallel architectures], Paris. [{{SERVER}}/files/scemama/Tutorial_QMC=Chem.pdf Slides available here] | ||
| + | |||
| + | * November 2012: Our results were presented for the 5 years of GENCI (Paris). | ||
| + | |||
| + | * October 2012: QMC=Chem was presented at the [http://services-numeriques.unistra.fr/hpc.html Equip@Meso meeting] "Chimie et sciences de la vie : de la simulation numérique au HPC", Strasbourg | ||
| + | |||
| + | * July 2012: QMC=Chem was presented at the [http://nkl.cc.u-tokyo.ac.jp/VECPAR2012/ VECPAR 2012] Conference, Kobe. | ||
| + | |||
| + | * June 2012: QMC=Chem was presented on the Intel booth at the International Supercomputing Conference 2012, Hamburg. | ||
| + | |||
| + | * March 2012: Beta-amyloid results presented for the Intel Xeon E5 release. [http://www.intel.com/content/dam/www/public/us/en/documents/case-studies/high-performance-xeon-e5-2680-genci-study.pdf Read more] | ||
| + | |||
| + | * Dec 2011: Two structures of a beta-amyloid involved in Alzheimer's disease were simulated on [http://www-hpc.cea.fr/fr/complexe/tgcc-curie.htm Curie (TGCC, France)] with QMC=Chem using up to 76 800 cores. 38.5% of the peak performance of the machine (960 TFlops/s) was obtained. | ||
| − | [ | + | * Nov 2011: Performance of QMC=Chem presented at Supercomputing 2011 in [http://sc11.supercomputing.org/schedule/event_detail.php?evid=bof156 BoF session “1000 x 0 = 0. Single-node optimisation does matter.”] |
| − | + | == QMC in a few words == | |
| − | == | ||
| − | + | Quantum Monte Carlo (QMC) is a set of probabilistic approaches for solving the Schrödinger equation. In short, QMC consists in simulating the probabilities of quantum mechanics by using the probabilities of random walks (Brownian motion and its generalizations). During the simulations each electron is moved randomly and quantum averages are computed as ordinary averages. | |
| − | + | <br style="clear: both" /> | |
| + | [[File:Qmc.png|400px|center]] | ||
| + | [[File:qmc_hydrogen.png|1000px|center]] | ||
| − | + | In practice, the major steps of a QMC simulation are as follows (See, Figure):<br> | |
| + | <B>Input</B>: The molecular geometry, the number of electrons, and an approximate electronic trial wave function, ψ<sub>T</sub>, obtained from a preliminary DFT or ab initio wave function-based calculation.<br> | ||
| + | <B> At each Monte Carlo step </B>: The values of ψ<sub>T</sub>, its gradient, and its Laplacian calculated at each spatial configuration (<B>r</B><sub>1</sub>,<B>r</B><sub>2</sub>, ...,<B>r</B><sub>N</sub>).<br> | ||
| + | <B>Output</B>: Quantum averages as ordinary averages along stochastic trajectories.<br> | ||
| − | + | <font color="red"> Key property of QMC : Fully parallelizable.</font>. This property could be critical in making QMC a successful approach. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | be | ||
| − | |||
| − | |||
| − | + | [http://qmcchem.ups-tlse.fr/files/caffarel/qmc_eacm.pdf '''More about quantum Monte Carlo methods in chemistry here'''] | |
| − | + | <br style="clear: both" /> | |
| + | __NOTOC__ | ||
| − | + | == QMC an alternative to DFT or post-HF methods ? == | |
| − | |||
| − | + | In practice, both DFT and post-Hartree-Fock approaches and their numerous variants rely on solving (very) large linear systems using iterative algorithms, where the finite dimension of the eigenvectors may become very large and is limited in practice to a few billion of components due to the finite aspects of the hardware. Because of such a mathematical structure, present intensive simulations of computational chemistry are characterized by i) the need of important computational resources both in terms of CPU and central memory requirements, ii) massive I/O, and iii) unavoidable frequent communications between processors. As a consequence, the algorithms are by their very nature extremely difficult to parallelize. Although computational chemistry is very present on HPC platforms as illustrated above, it is difficult to envision how standard algorithms could take advantage in the near future of massively parallel platforms (exascale) and cloud computing. | |
| − | |||
| − | |||
| + | === DFT === | ||
| − | + | <font color="blue">Advantages</font>: | |
| − | + | <ul> | |
| − | + | <li> The fully-correlated N-body electronic problem is replaced by | |
| − | + | an effective one-body problem. Only approximation: Choice of the effective (exchange-correlation) potential, | |
| − | + | a point leading to various levels of accuracy (local DFT, gradient-corrected DFT, hybrid DFT, etc...). One-body framework particularly attractive for interpreting electronic processes in a simple manner using one-electron pictures. | |
| − | + | <li> Computational effort of DFT has a very good scaling, of order <math>O(N^3)</math> where N is the number of electrons. | |
| − | |||
| − | |||
| − | + | <li> The various exchange-correlation potentials developped have now reached an accuracy allowing reasonable quantitative results, even for (very) large molecular systems. | |
| + | </ul> | ||
| + | <font color="blue">Limitation</font>: Strong limitation of DFT: the error made is not controlled and there is no known procedure to reduce it in a systematic way. | ||
| − | === | + | === Post-HF methods === |
| − | + | Post-HF = expansion of the wave function over a sum of | |
| + | antisymmetrized products of one-particle orbitals | ||
| − | + | Popular versions: MP2, MPn, CCSD(T), CI, MRCI, etc. | |
| − | + | In contrast with DFT: Error much more easy to control but price to pay very high (defavorable scaling). | |
| − | + | === QMC: an alternative approach? === | |
| − | |||
| − | |||
| − | |||
| − | + | <font color="blue">Advantages:</font> | |
| + | <ul> | ||
| + | <li> Method easy to implement and having a very favorable scaling, typically <math>O(N^3)</math>. | ||
| − | + | <li> Accurate total energies. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <li> Unlike DFT and post-HF methods, QMC ideally suited to High Performance Computing (HPC) (very modest central memory requirements, very limited input/output flows, codes perfectly parallelized). | |
| − | + | </ul> | |
| + | <font color="blue">Present limitations:</font> | ||
| + | <ul> | ||
| + | <li> The only systematic error left -the fixed-node error- may have an important impact when <EM> differences </EM> of energies are considered. The heavy compensation of errors at work in both DFT and post-HF schemes is much less effective in Fixed-Node QMC calculations. | ||
| − | + | <li> No general and robust algorithm for computing forces in QMC. | |
| − | |||
| − | |||
| − | + | <li> No simple and systematic way of constructing complex trial wavefunctions of good quality without massive parameter reoptimizations. No "black-box" way for QMC. | |
| − | + | </ul> | |
Latest revision as of 14:45, 13 July 2015
This website is devoted to the scientific and software activities of the quantum Monte Carlo (QMC) group of Toulouse, France. The grand objective of our project is to make of QMC an alternative and efficient tool for electronic structure in chemistry. Our group -- headed by Michel Caffarel -- is located at the Laboratoire de Chimie et Physique Quantiques, CNRS and Université Paul Sabatier.
The QMC=Chem project is supported by the french Agence Nationale de la Recherche Scientifique (ANR) under Grant No. ANR2011 BS08 004 01
News
- December 2014: QMC=Chem was selected for the France-Grilles Cloud Challenge. Video
- June 2014: QMC=Chem was selected for a meso-challenge on the new CALMIP system EOS. 12000 cores ran for 48 hours.
- July 2013: QMC=Chem tutorial, Cecam workshop Atomistic and molecular simulations on massively parallel architectures, Paris. Slides available here
- November 2012: Our results were presented for the 5 years of GENCI (Paris).
- October 2012: QMC=Chem was presented at the Equip@Meso meeting "Chimie et sciences de la vie : de la simulation numérique au HPC", Strasbourg
- July 2012: QMC=Chem was presented at the VECPAR 2012 Conference, Kobe.
- June 2012: QMC=Chem was presented on the Intel booth at the International Supercomputing Conference 2012, Hamburg.
- March 2012: Beta-amyloid results presented for the Intel Xeon E5 release. Read more
- Dec 2011: Two structures of a beta-amyloid involved in Alzheimer's disease were simulated on Curie (TGCC, France) with QMC=Chem using up to 76 800 cores. 38.5% of the peak performance of the machine (960 TFlops/s) was obtained.
- Nov 2011: Performance of QMC=Chem presented at Supercomputing 2011 in BoF session “1000 x 0 = 0. Single-node optimisation does matter.”
QMC in a few words
Quantum Monte Carlo (QMC) is a set of probabilistic approaches for solving the Schrödinger equation. In short, QMC consists in simulating the probabilities of quantum mechanics by using the probabilities of random walks (Brownian motion and its generalizations). During the simulations each electron is moved randomly and quantum averages are computed as ordinary averages.
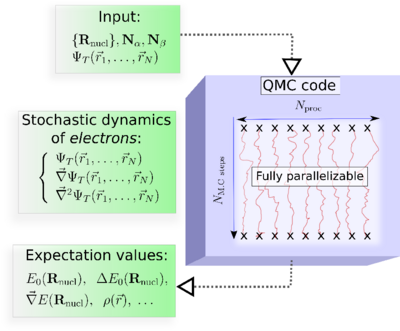
In practice, the major steps of a QMC simulation are as follows (See, Figure):
Input: The molecular geometry, the number of electrons, and an approximate electronic trial wave function, ψT, obtained from a preliminary DFT or ab initio wave function-based calculation.
At each Monte Carlo step : The values of ψT, its gradient, and its Laplacian calculated at each spatial configuration (r1,r2, ...,rN).
Output: Quantum averages as ordinary averages along stochastic trajectories.
Key property of QMC : Fully parallelizable.. This property could be critical in making QMC a successful approach.
More about quantum Monte Carlo methods in chemistry here
QMC an alternative to DFT or post-HF methods ?
In practice, both DFT and post-Hartree-Fock approaches and their numerous variants rely on solving (very) large linear systems using iterative algorithms, where the finite dimension of the eigenvectors may become very large and is limited in practice to a few billion of components due to the finite aspects of the hardware. Because of such a mathematical structure, present intensive simulations of computational chemistry are characterized by i) the need of important computational resources both in terms of CPU and central memory requirements, ii) massive I/O, and iii) unavoidable frequent communications between processors. As a consequence, the algorithms are by their very nature extremely difficult to parallelize. Although computational chemistry is very present on HPC platforms as illustrated above, it is difficult to envision how standard algorithms could take advantage in the near future of massively parallel platforms (exascale) and cloud computing.
DFT
Advantages:
- The fully-correlated N-body electronic problem is replaced by an effective one-body problem. Only approximation: Choice of the effective (exchange-correlation) potential, a point leading to various levels of accuracy (local DFT, gradient-corrected DFT, hybrid DFT, etc...). One-body framework particularly attractive for interpreting electronic processes in a simple manner using one-electron pictures.
- Computational effort of DFT has a very good scaling, of order <math>O(N^3)</math> where N is the number of electrons.
- The various exchange-correlation potentials developped have now reached an accuracy allowing reasonable quantitative results, even for (very) large molecular systems.
Limitation: Strong limitation of DFT: the error made is not controlled and there is no known procedure to reduce it in a systematic way.
Post-HF methods
Post-HF = expansion of the wave function over a sum of antisymmetrized products of one-particle orbitals
Popular versions: MP2, MPn, CCSD(T), CI, MRCI, etc.
In contrast with DFT: Error much more easy to control but price to pay very high (defavorable scaling).
QMC: an alternative approach?
Advantages:
- Method easy to implement and having a very favorable scaling, typically <math>O(N^3)</math>.
- Accurate total energies.
- Unlike DFT and post-HF methods, QMC ideally suited to High Performance Computing (HPC) (very modest central memory requirements, very limited input/output flows, codes perfectly parallelized).
Present limitations:
- The only systematic error left -the fixed-node error- may have an important impact when differences of energies are considered. The heavy compensation of errors at work in both DFT and post-HF schemes is much less effective in Fixed-Node QMC calculations.
- No general and robust algorithm for computing forces in QMC.
- No simple and systematic way of constructing complex trial wavefunctions of good quality without massive parameter reoptimizations. No "black-box" way for QMC.