Difference between revisions of "Quantum Monte Carlo for Chemistry @ Toulouse"
| Line 14: | Line 14: | ||
<B>Output</B>: Quantum averages as ordinary averages along stochastic trajectories.<br> | <B>Output</B>: Quantum averages as ordinary averages along stochastic trajectories.<br> | ||
| − | <font color="red"> Key property of QMC : Fully parallelizable | + | <font color="red"> Key property of QMC : Fully parallelizable.</font>. This property could be critical in making QMC successful. |
[[Much more about QMC here]] | [[Much more about QMC here]] | ||
<br style="clear: both" /> | <br style="clear: both" /> | ||
Revision as of 16:50, 24 October 2010
This website is devoted to the scientific and software activities of the quantum Monte Carlo (QMC) group of Toulouse, France. The grand objective of our project is to make of QMC an alternative and efficient tool for electronic structure in chemistry. Our group -- headed by Michel Caffarel -- is located at the Laboratoire de Chimie et Physique Quantiques, CNRS and Université Paul Sabatier.
QMC in a few words
Quantum Monte Carlo (QMC) is a set of probabilistic approaches for solving the Schrödinger equation. In short, QMC consists in simulating the probabilities of quantum mechanics by using the probabilities of random walks (Brownian motion and its generalizations). During the simulations each electron is moved randomly and quantum averages are computed as ordinary averages.
In practice, the major steps of a QMC simulation are as follows:
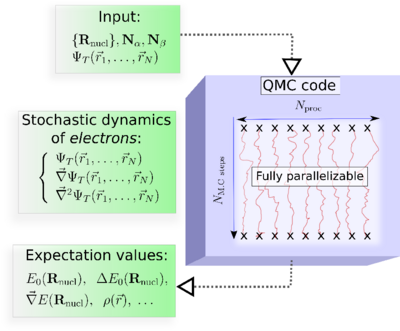
Input: The molecular geometry, the number of electrons, and an approximate electronic trial wave function, ψT, obtained from a preliminary DFT or ab initio wave function-based calculation.
At each Monte Carlo step : The values of ψT, its gradient, and its Laplacian calculated at each spatial configuration (r1,r2, ...,rN).
Output: Quantum averages as ordinary averages along stochastic trajectories.
Key property of QMC : Fully parallelizable.. This property could be critical in making QMC successful.
Much more about QMC here
QMC an alternative to DFT or post-HF methods ?
Two standard approaches in computational chemistry:
-Density Functional Theory (DFT)
-Post-Hartree-Fock (post-HF) methods.
Attractive features of DFT
i.) In DFT the fully-correlated N-body electronic problem is replaced by an effective one-body problem (nuclei attraction + average electrostatic electronic repulsion + exchange-correlation potential). The only approximation made is the choice of the exchange-correlation potential, a point which leads to various levels of accuracy for DFT :local DFT, gradient-corrected DFT, hybrid DFT, etc.. Such a one-body framework is particularly attractive at the conceptual level since electronic processes can be interpreted in a simple manner using one-electron pictures, a point which is clearly in sharp contrast with wavefunction-based approaches (post-HF methods) where (very) large determinantal expansions have almost no physical meaning.
ii.) Thanks to this one-body formalism the computational effort of DFT has also a very good scaling, the typical scaling being of order <math>O(N^3)</math> where N is the number of electrons.
iii.) The various exchange-correlation potentials developped in the last years have now reached a point where reasonable quantitative results can be obtained, even for a large molecular systems.
Limitation of DFT
However, DFT has also a strong limitation related to the fact that the error made in such calculations is basically not controlled and that there exists no known procedure to reduce it in a systematic way.
Regarding post-Hartree-Fock methods, they are quite different from DFT and are based on the expansion of the wavefunction over a sum of
antisymmetrized products of one-particle orbitals, the various parameters entering the expansion being optimized
by using the variational principle. Many variants of these methods exist. Among the most famous ones we can cite the CCSD(T) approaches
well-adapted to systems having a strong mono-configurational character and the MRCI approaches used when multi-configurational effects are
significant.
In contrast with DFT, the error is now much more easy to control but, unfortunately, the price to pay for that is in general too high.
Indeed, typical scalings [for example, N7 for CCSD(T)] forbid to attack systems beyong those of intermediate sizes (let us say more than one
hundred active electrons).
In conclusion, it can be legitimately considered that there does not exist a satisfactory electronic approach combining both efficiency and accuracy for (very) large molecular systems.
The project presented here is an attempt to promote an alternative third way: the quantum Monte Carlo approach
The advantages of QMC are indeed attractive:
i.) Like DFT, the method is simple to implement and has a very favorable scaling (typicallly, O(N3) for a general system).
ii.) Like post-HF methods, the accuracy is in general very good.
iii.) Unlike DFT and post-HF methods, QMC is particularly well-adapted to High Performance Computing (HPC): central memory requirements are very modest and bounded (no increase of memory as a function of some parameter like the basis set size in post-HF), the Input/Output flows are very limited, and the codes are perfectly parallelized (QMC codes can be easily implemented on massively parallel machines, on heterogeneous grids, etc. ).
Unfortunately, QMC has also some strong limitations :
i.) Besides the usual statistical error inherent to any Monte Carlo scheme and which can be easily controlled (for example, by making longer and longer simulations), there is some systematic error left, known as the fixed-node error. Although this error is small in terms of total energis, it can play a central role when differences of energies are considered. Unfortunately, it is well-known that differences of energies are at the very center of chemistry (e.g., electronic affinities, ionization potentials, binding energies, reaction barriers, etc.). Numerical experience has shown that the compensations of errors at work in both DFT and post-HF schemes are in general much important than in Fixed-Node QMC calculations.
ii.) In contrast with DFT and post-HF there does not exist yet a general and robust algorithm for computing forces in QMC (gradients of total energy with respecti to nuclear coordinates).
iii.) For large molecular systems, there is no simple and systematic way of constructing trial wavefunctions of good quality without reoptimizing for each system a very large number of variational parameters. This aspect forbids to apply QMC approach in a "black-box" way, thus strongly hampering the diffusion of QMC techniques into the general computational chemistry community.
In short, the main objectives of our project are to circumvent the previous limitations to make of QMC a popular approach in computational chemistry.