Quantum Monte Carlo for Chemistry @ Toulouse
This website is devoted to the scientific and software activities of the quantum Monte Carlo (QMC) group of Toulouse, France. The grand objective of our project is to make of QMC an alternative and efficient tool for electronic structure in chemistry. Our group -- headed by Michel Caffarel -- is located at the Laboratoire de Chimie et Physique Quantiques, CNRS and Université Paul Sabatier.
QMC in a few words
Quantum Monte Carlo (QMC) is a set of probabilistic approaches for solving the Schrödinger equation. In short, QMC consists in simulating the probabilities of quantum mechanics by using the probabilities of random walks (Brownian motion and its generalizations). During the simulations each electron is moved randomly and quantum averages are computed as ordinary averages.
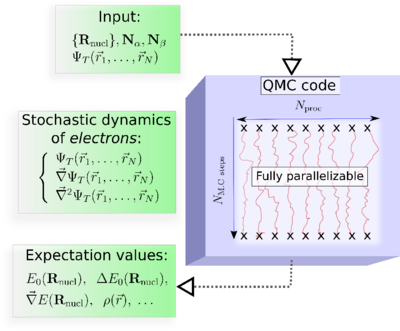
In practice, the major steps of a QMC simulation are as follows (See, Figure):
Input: The molecular geometry, the number of electrons, and an approximate electronic trial wave function, ψT, obtained from a preliminary DFT or ab initio wave function-based calculation.
At each Monte Carlo step : The values of ψT, its gradient, and its Laplacian calculated at each spatial configuration (r1,r2, ...,rN).
Output: Quantum averages as ordinary averages along stochastic trajectories.
Key property of QMC : Fully parallelizable.. This property could be critical in making QMC a successful approach.
QMC an alternative to DFT or post-HF methods ?
Two standard approaches in computational chemistry:
- Density Functional Theory (DFT) , the most widely used approach
- Wave function-based post-Hartree-Fock (post-HF) methods
DFT
Advantages:
1.) The fully-correlated N-body electronic problem is replaced by
an effective one-body problem. Only approximation: Choice of the effective (exchange-correlation) potential,
a point leading to various levels of accuracy (local DFT, gradient-corrected DFT, hybrid DFT, etc...). One-body framework particularly attractive for interpreting electronic processes in a simple manner using one-electron pictures.
2.) Computational effort of DFT has a very good scaling, of order <math>O(N^3)</math> where N is the number of electrons.
3) The various exchange-correlation potentials developped have now reached an accuracy allowing reasonable quantitative results, even for (very) large molecular systems.
Limitation:
Strong limitation of DFT: the error made is not controlled and there is no known procedure to reduce it in a systematic way.
Post-Hartee-Fock methods
Post-HF: Expansion of the wave function over a sum of antisymmetrized products of one-particle orbitals, the various parameters entering the expansion being optimized by using the variational principle.
Popular versions: MP2, MPn, CCSD(T), CI, MRCI, etc.
In contrast with DFT: error much more easy to control
However, price to pay very high: Scalings defavorable.
Quantum Monte Carlo: an alternative approach?
Advantages:
i.) Method easy to implement and having a very favorable scaling, typically O(N3).
ii.) Very good accuracy.
iii.) Unlike DFT and post-HF methods, QMC particularly well-adapted to High Performance Computing (HPC): Central memory requirements very modest (only linear increase as a function of the number of electrons), Input/Output flows very limited, and codes perfectly parallelized.
Present strong limitations:
i.) The only one systematic error left -the fixed-node error- although very small in general can play a central role when differences of energies are considered. Numerical experience has shown that the compensations of
errors at work in both DFT and post-HF schemes are in general much important than in Fixed-Node QMC calculations.
ii.) In contrast with DFT and post-HF there does not exist yet a general and robust algorithm for computing forces in QMC (gradients of total energy with respecti to nuclear coordinates).
iii.) For large molecular systems, there is no simple and systematic way of constructing trial wavefunctions of good quality without reoptimizing for each system a very large number of variational parameters. This aspect forbids to apply QMC approach in a "black-box" way, thus strongly hampering the diffusion of QMC techniques into the general computational chemistry community.